
GAME CONCEPT
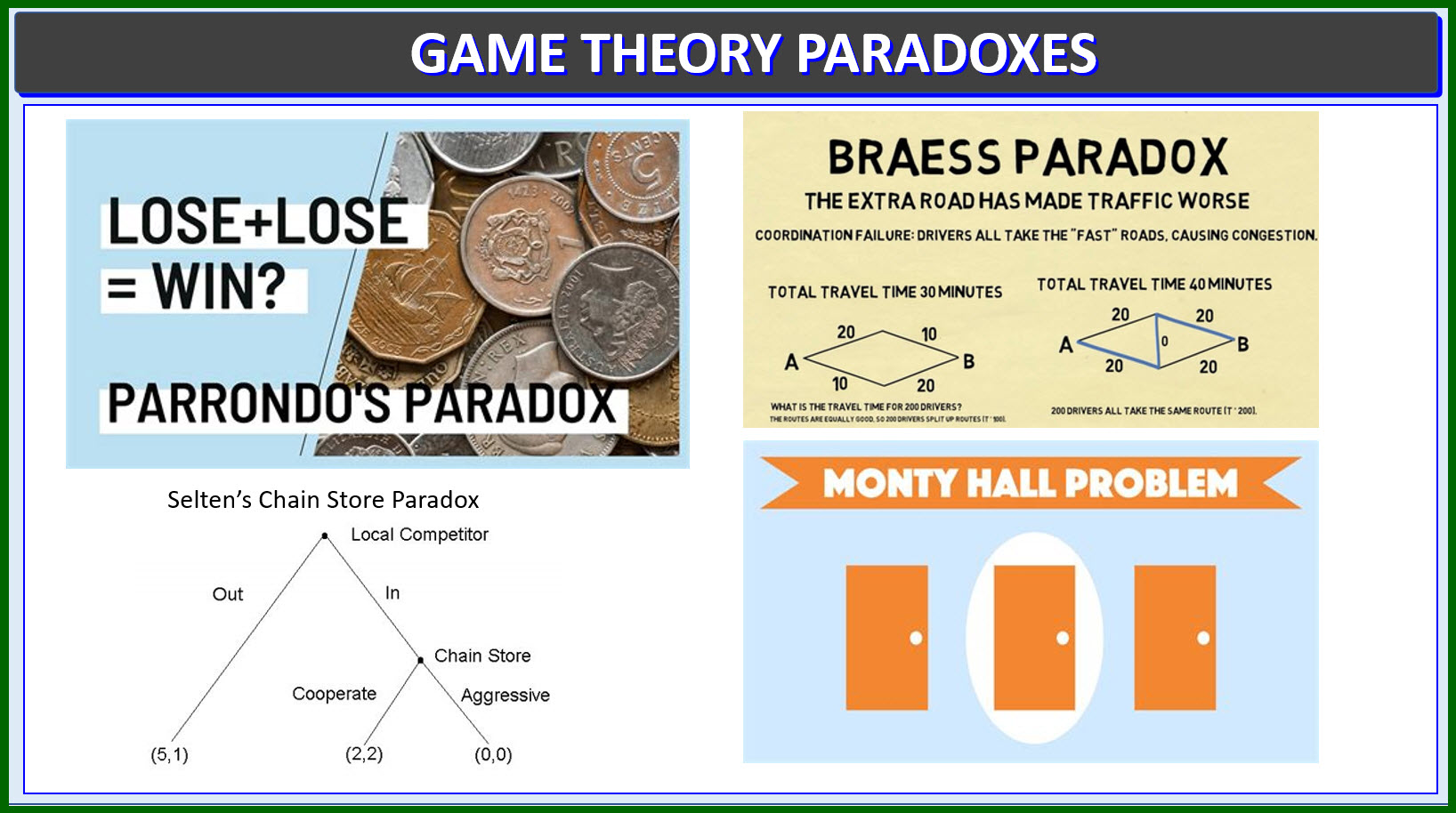
There are four famous paradoxes in Game Theory: Braess Paradox,
The Monty Hall problem, Selten's Chain Store Paradox and
Parrondo's Paradox. The Braess Paradox relates to road networks.
The Monty Hall problem is a game show paradox. Selten's Chain
Store Paradox is about a chain store and local competitor.
Parrondo's paradox was discovered by Spanish physicist Juan
Parrondo in 1996. It described a paradoxical situation where
two losing strategies when combined can become a winning
strategy. It has found applications in engineering, population
dynamics, ecology, and financial risk. Explanation examples
typically involve weighted coins that individually flipped only
yield losing results; however, when combined can produce a
winning strategy.
This Tech Deck game explores Parrondo's Paradox. In
Paradoxical, players juggle losing strategies to find a winning
combination. Players try to uncover paradoxes through playing
combinations of cards from two decks that on their own have only
losing strategies. Each turn, players take actions to try to
discover a Parrondo paradox from decks of cards that individually
would produce strictly losing outcomes but when combined allows
for the possibility of a winning strategy.
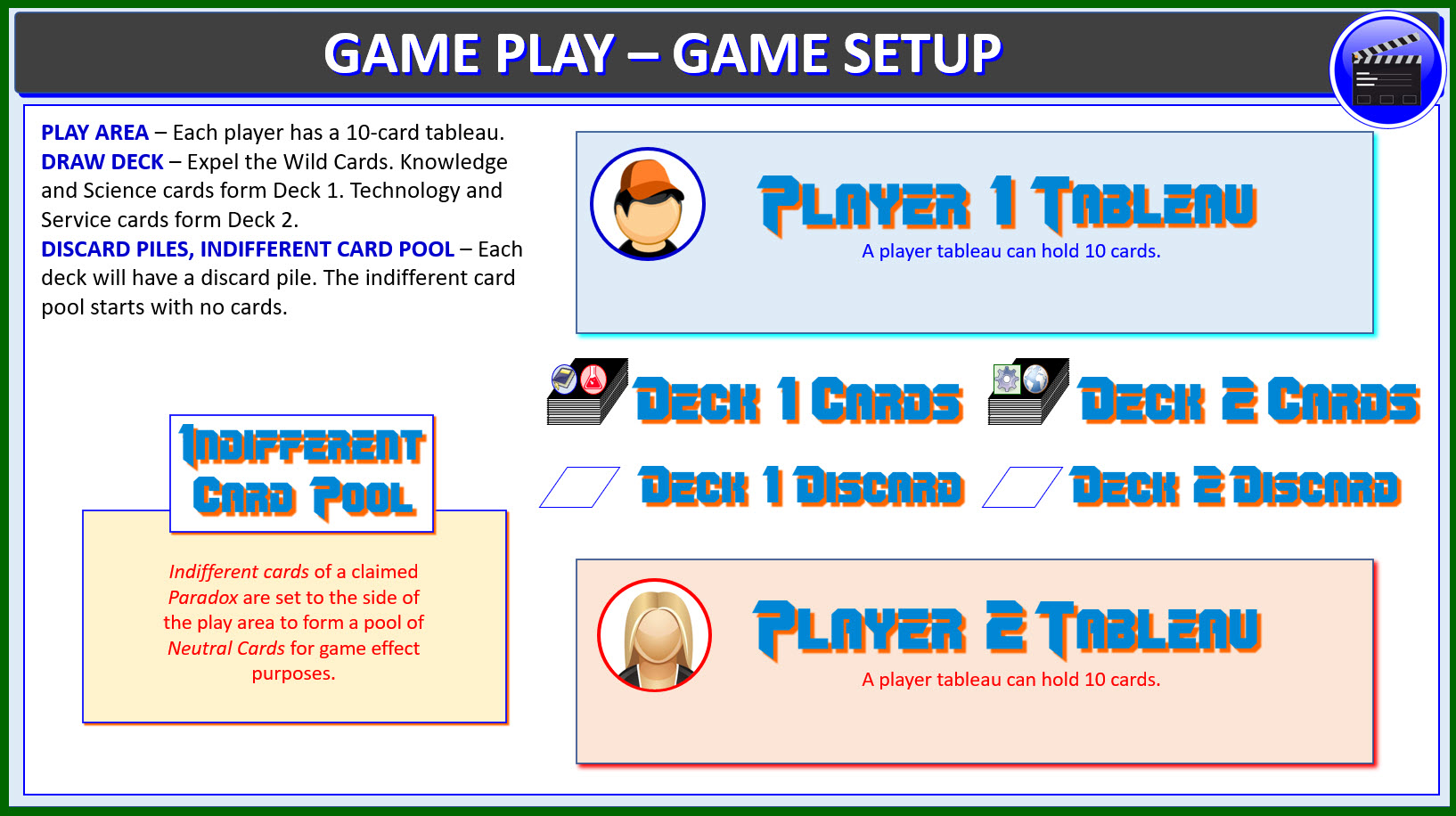
GAME SETUP
PLAY AREA -
Each player has a 10-card tableau (that starts with no cards
in it).
DRAW DECK -
Expel the Wild Cards. Cull the Knowledge and Science domain
cards to form Deck 1. The remaining Technology and Service
domain cards form Deck 2.
DISCARD PILES, INDIFFERENT CARD POOL -
Each deck will have a discard pile (that starts with no cards
in it). Finally, to the side of the play area is the Indifferent
Card Pool (that starts with no cards in it).
PARADOXICAL GAME PLAY OVERVIEW

On a player's turn, they take one of four actions: Build
tableau, Claim paradox, Use Card Effect, or Add to Tableau:
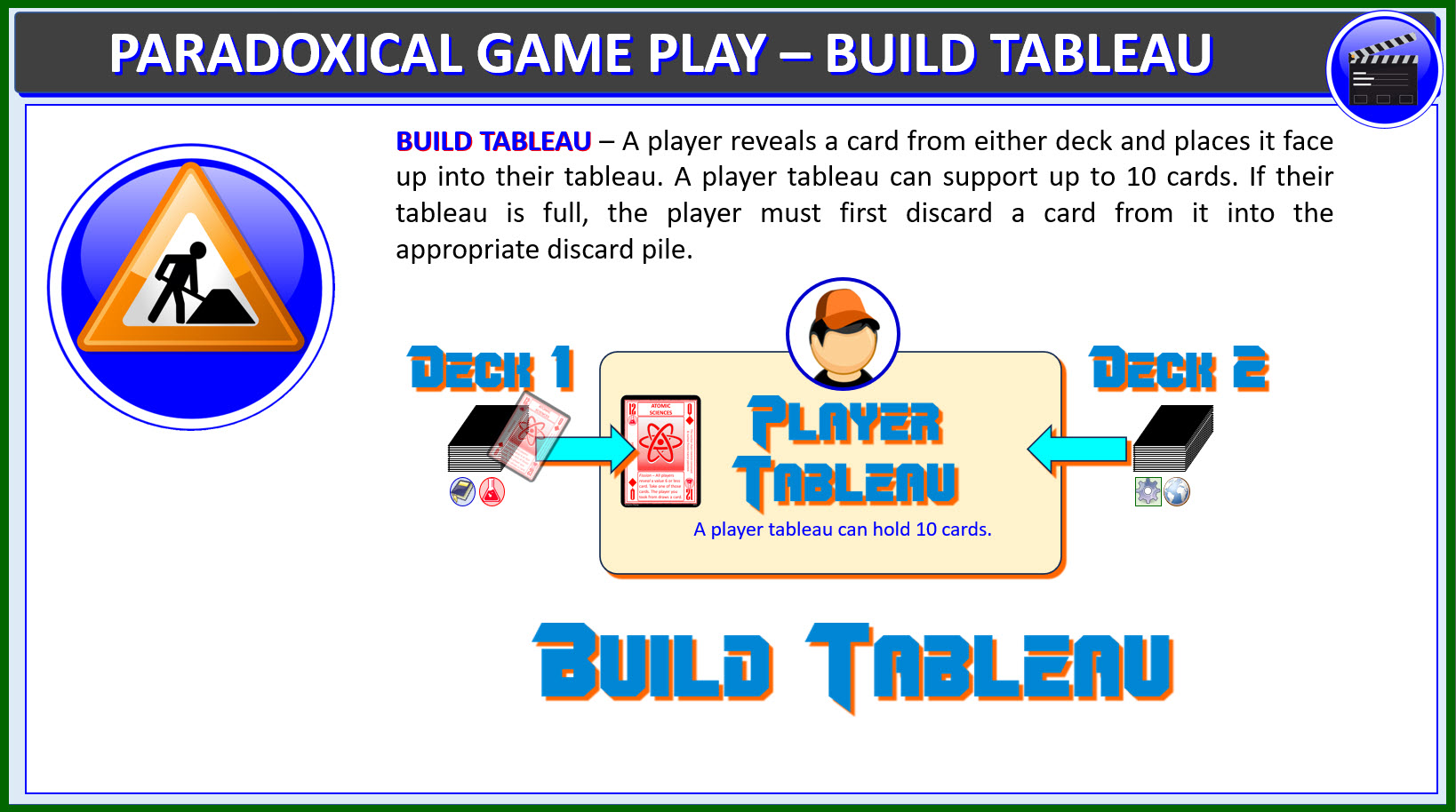
BUILD TABLEAU -
A player reveals a card from either deck and places it face
up into their tableau. A player tableau supports up to 10
cards. If their tableau is full, the player must first discard
a card from it into the appropriate discard pile. If any deck
runs out, reshuffle its discard pile and cards with matching
domains in the indifferent card pool to form a new draw deck.
CLAIM PARADOX -
Identify the valid paradox in your tableau (see below).
Afterwards, the indifferent cards of the paradox are placed
to the side of the play area and become Neutral Cards that
can be affected and used by Card Effects. The Indifferent
Card Pool can hold up to 5 cards. If it exceeds 5 cards, the
active player discard cards from the pool until there are only
5 cards left. After a player claims a 10-card paradox (full
house or straight), they draw 3 cards (from either draw deck)
and puts up to two cards from their hand into their Tableau.
Give the player a token denoting they have claimed a paradox.
If this is the second paradox they have claimed, they
immediately win the game.

USE CARD EFFECT -
Use a Card Effect from a card in your hand or a card in your
tableau (see below).

ADD TO TABLEAU -
A player reveals a card from their hand and adds it face up
to their tableau. A player tableau can hold up to 10 cards.
If their tableau is full, the player must first discard a
card from it into the appropriate discard pile. Note: players
start the game with no cards in hand, but they can get cards
via Tech Deck game effects.

PLAY PASSES -
After a player has taken an action, play passes to the next
player on the left and they become the active player.
VALID PARADOX
VALID PARADOX -
A valid paradox has either 8 cards or 10 cards made from face
up tableau cards. A paradox is composed of set cards, and an
equivalent number of indifferent cards which serve as a
counterweight to the set cards. The set cards are composed of
either two pairs, a pair and a triple (full house), or a
straight (sequence). The indifferent cards can be of any value
and domain. Read Loki and theft of the Mighty Sword of Avalon
introduction story to all the players.
TWO PAIR PARADOX
This 8-card paradox is comprised of a set of two pairs and
four accompanying indifferent cards. Each card in each pair
must be from a different deck. Thus, one card in the pair
must be a Knowledge or Science domain card, and the other must be a
Technology or Service domain card. The sum value of the set cards must
be higher than the sum value of the indifferent cards. If set
cards had positive value, the indifferent ones negative, their
total must be positive.
FULL HOUSE PARADOX -
This 10-card paradox is comprised of 5 set cards (one pair
and a triple), and five accompanying indifferent cards. Each
card in the pair must be from a different deck. The sum value
of the set cards must exceed the sum value of the indifferent
cards. Expressed in a paradoxical way, if the set cards (pair
& triple) had positive values and the indifferent cards had
negative values, the total sum value of all the cards in the
paradox must be positive.
STRAIGHT (SEQUENCE) PARADOX -
This 10-card paradox has 5 set cards that form a numerical
sequence (e.g., 5-6-7-8-9), and five indifferent cards (of
any value and domain). Cards in the sequence must be from
different decks. The sum value of the set cards must exceed
the sum value of the indifferent cards. Put in another way,
if the set cards all had positive values and the indifferent
cards all had negative values, the total sum value of all the
cards must be positive.
PARADOXICAL GAME PLAY EXAMPLE
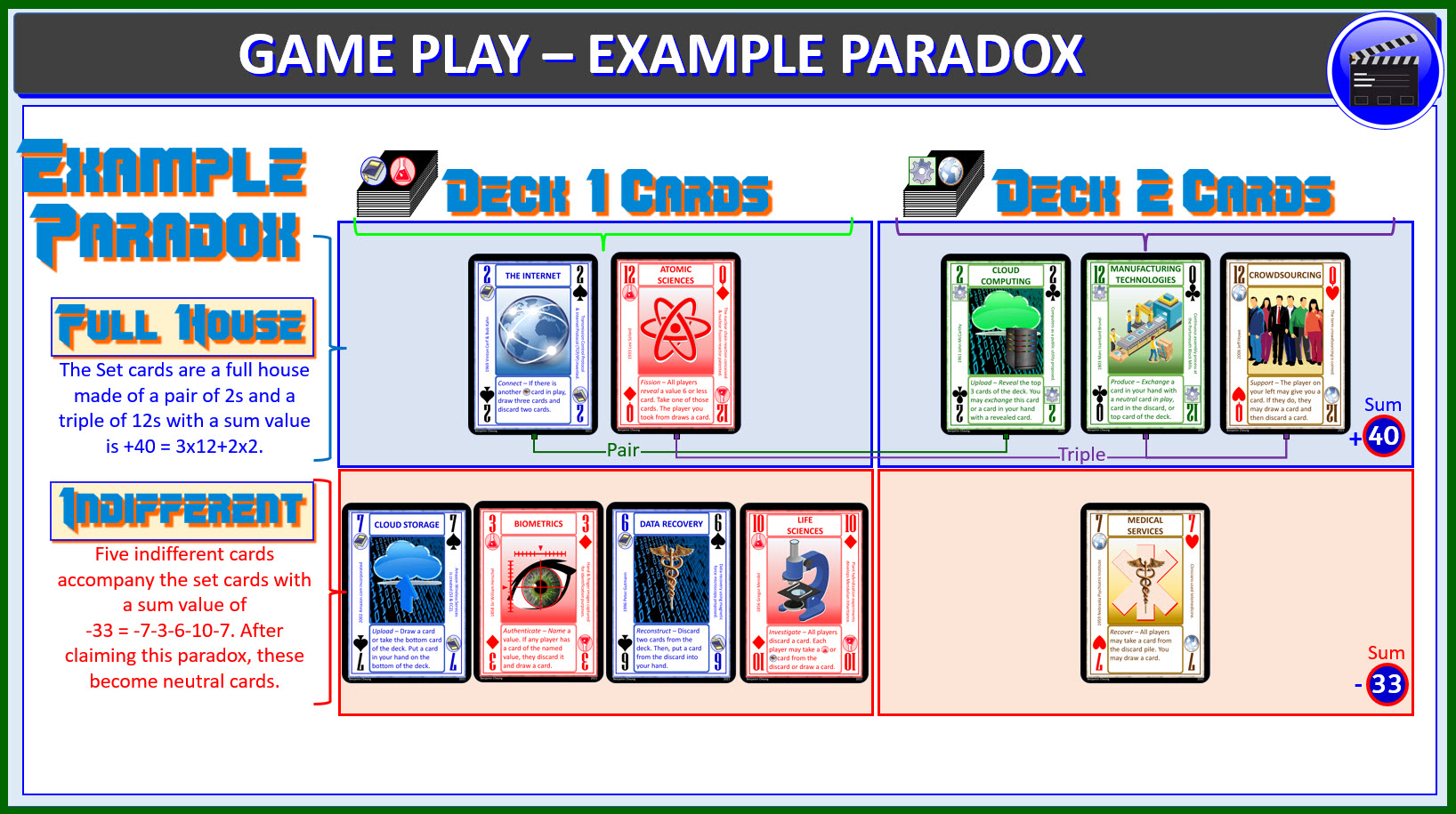
Paradoxical Game Play Example
The following diagram shows an example of claiming a paradox.
The tableau of Player #1 has a 2,6,7 of Knowledge, 3, 10, 12
of Science, and 2, 12 of Technology and 7,12 of Service. The
cards on the left were drawn from Deck 1 and the cards on the
right were drawn from Deck 2. The Set cards are a full house
(a pair of 2s and a triple of 12s). There are also 5 indifferent
cards that accompany the Full House to form a Paradox. For
this to be a valid Paradox, the set cards (Full House) value
(40) must have a sum which is greater than the indifferent
card sum (33). In this case, 40 > 33, so this is a valid Paradox.
Player #1 can use his action to Claim this Full House Paradox.
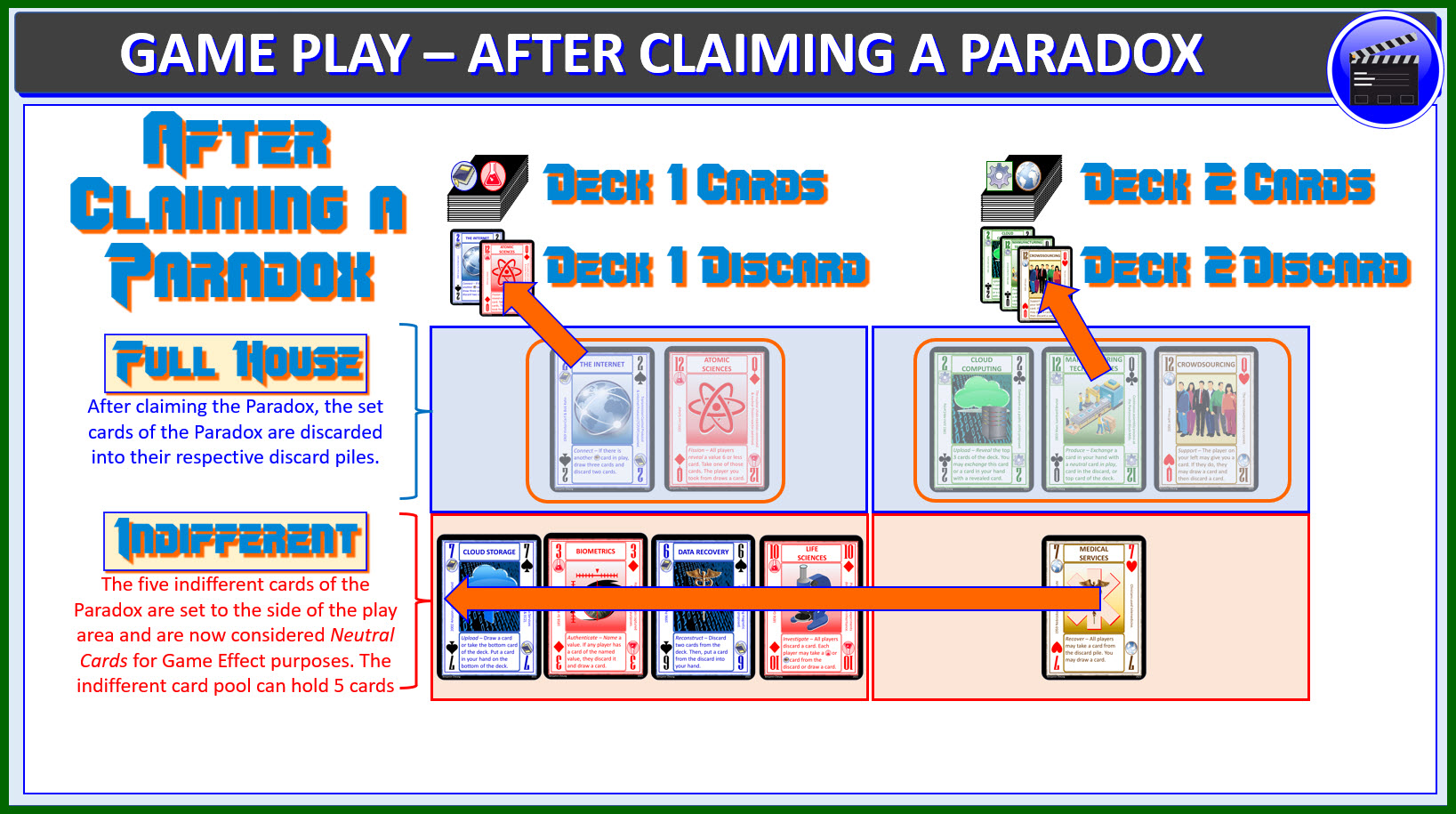
After Claiming a Paradox
After a Player claims a valid Paradox, the set cards of the
Paradox are discarded into their respective discard piles. The
five indifferent cards of the Paradox are set to the side of
the play area and are now considered Neutral Cards for Game
Effect purposes. The indifferent card pool can hold 5 cards.
If there are more than 5 cards in the Indifferent Card Pool,
the active player chooses which cards to discard into their
respective discard piles until there are only 5 cards left
in the Indifferent Card Pool.
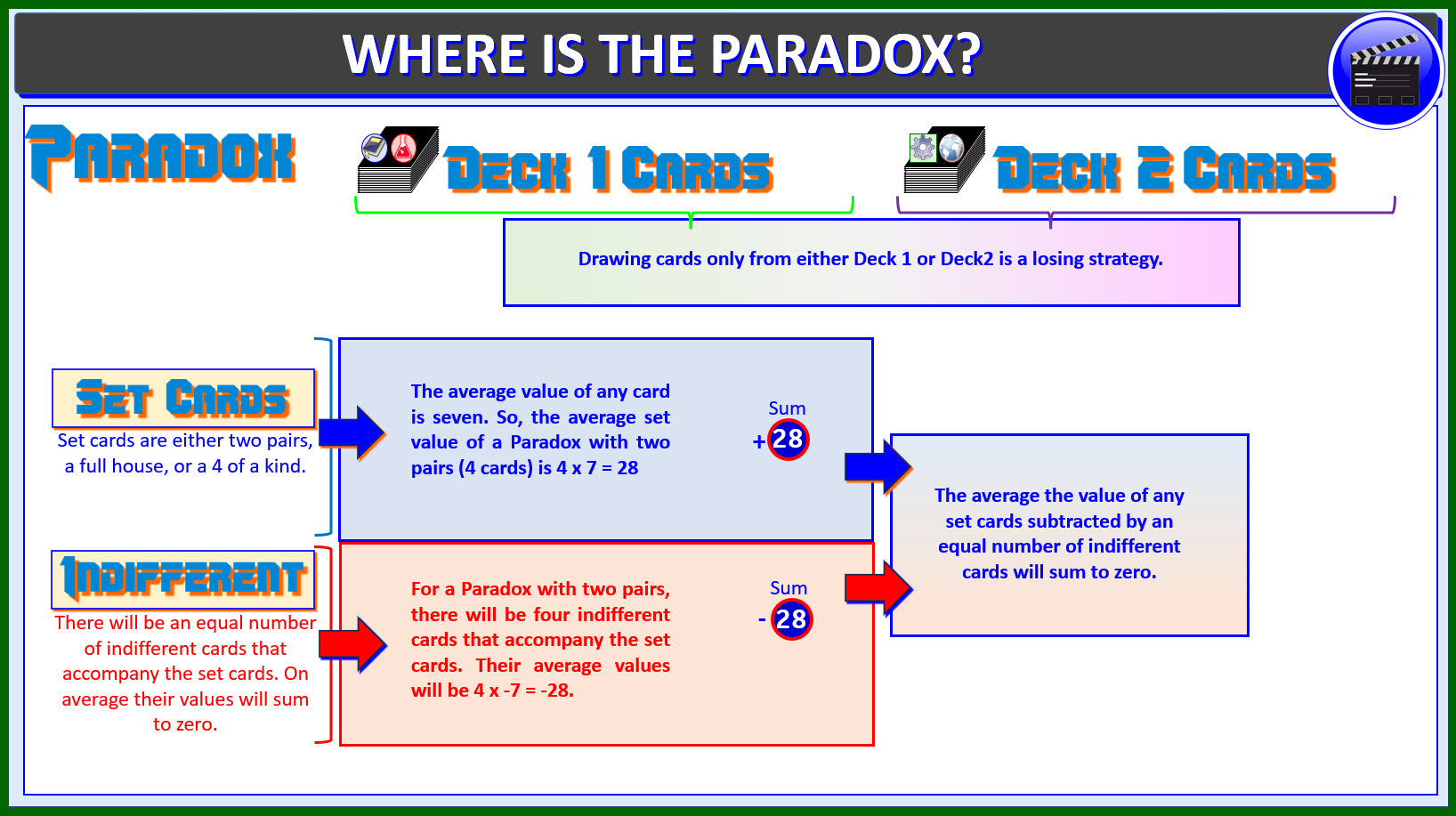
WHERE IS THE PARADOX?
Where is Parrondo's Paradox in a Paradoxical Paradox?
Where is Parrondo's Paradox
Where is Parrondo's Paradox in a Paradoxical Paradox?
To see that you have to consider what the average value
of a card in the deck is. The sum value of all the cards
in a deck is 364. If you divide that by 52 it equals 7.
You can also see this if you take the first card and last
card in a domain (1+13), their average value is 7 because
14/2 = 7. A Paradoxical Paradox is defined such that
it must have set cards that come from different decks.
There are either 4 or 5 set cards. If every card has an
average value of 7, then 4 or 5 set cards will have a sum
of 28 or 35 respectively. The set cards must be accompanied
by an equal number of indifferent cards whose sum will also
on average be 28 or 35. Thus, on average the sum value
of the set cards subtracted by the average sum value
of indifferent cards will sum to zero.
In Parrondo's Paradox two losing strategies when combined can
produce a winning strategy.
In Paradoxical if you only drew from either Deck 1 or Deck 2
you would never win because Paradoxical paradoxes are comprised
of cards from both decks. Thus two losing strategies come together
to create a winning strategy. Even then, it isn't easy because
you have to find set cards who sum value is higher than the sum
value of the indifferent cards which is paradoxical.
DOWNLOAD THE RULES
Paradoxical Full Rules:
Paradoxical Rules Full
Paradoxical Compact Rules:
Paradoxical Rules Compact
PARADOXICAL INTRODUCTION VIDEO
Click below to watch a introduction video for Paradoxical.
The introduction video describes the basic concepts,
objectives and an introduction to the Tech Deck.
PARADOXICAL PLAY GUIDE VIDEO
Watch a play guide video for Paradoxical. The play guide
video is an in depth video on how to setup the game,
and all the steps involved in playing the game.
ENTRY ON BOARD GAME GEEK
You can read and explore the
BoardGameGeek entry for Paradoxical.
PUBLICATION INFORMATION
·
Published: January 7, 2024
·
Format: Card Game
·
Elements: 54 Cards
·
Size: 3.75" x 2.8751" x .875"
ORDERING PARADOXICAL
·
To purchase the Tech Deck:
Contact Me
EXPLORE OTHER TECH DECK GAMES


















































